As well as creating DCPs from the content you specify, DCP-o-matic can also export projects to ProRes and MP4 files. This is most often useful to convert DCPs to a file that is smaller and easier to play back.

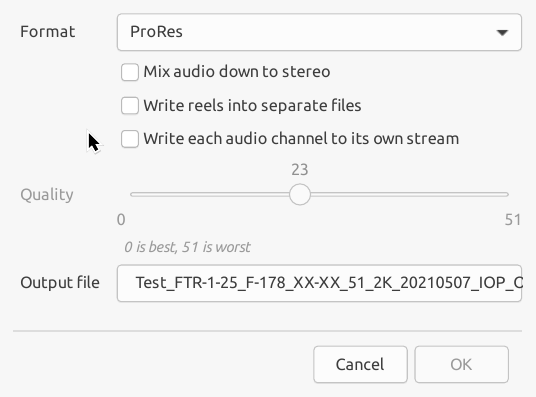
To convert a DCP to ProRes or MP4, the first step is start a new project and import the DCP (see Chapter 5, Manipulating existing DCPs). Then, choose Export... from the Jobs menu to open the export dialogue, as shown in Figure 9.1, “Export dialogue”.

From this dialogue you can select the required output format, output file and, in the case of MP4, the quality of the output file (by setting the CRF value).

The useful range of CRF values is from 17 (high quality but large file size) to 28 (smaller file size and still reasonable quality).

The time needed to export, and the resulting size, depend partly on the DCP resolution set in the project. To change that, see Chapter 7, DCP settings.

You can also choose whether to mix down multichannel sources to stereo and whether you want to write separate reels to separate files.